Понимание теории игр

Как использовать интеллект для прогнозирования поведения в будущем

Что, если бы вы могли спрогнозировать реакцию конкурентов на ваши действия? Смогли бы убедиться в их соответствии вашим интересам, прежде чем действовать? И, что еще лучше, если бы вы могли сделать это с помощью «научного» метода, а не догадок?

Понимание того, как люди будут реагировать на ваш выбор, важно во многих сферах бизнеса. Представьте, что вы конкурируете на рынке с несколькими компаниями. Если вы сможете предугадать их действия, тогда есть возможность либо отменить некоторые из них, либо обыграть их выбор.

Теория игр дает инструменты чтобы это обдумать.

Что такое теория игр

Теория игр — это обоснованная попытка предсказать поведение. Она применяется в ситуациях, когда успех человека в принятии решений зависит от выбора других людей. Простые модели включают в себя группу игроков, определение действий, которые эти игроки могут выбрать, и payoffs (выплаты), — сколько каждый игрок выиграет или проиграет за каждую комбинацию действий.

Джон фон Нейман и Оскар Моргенштерн определили основы теории игр в 1944 году своей работе «Теория игр и экономическое поведение».

Одновременные и последовательные игры

В теории игр есть две основные категории ситуаций:

1. Игры с одновременными ходами — здесь игроки делают свои ходы одновременно. Например, игра «камень-ножницы-бумага» или запуска конкурирующими компаниями новых продуктов в начале года.
2. Игры с последовательными ходами — игроки по очереди делают ходы. К ним относятся шахматы или ситуации, когда две конкурирующие компании по очереди реагируют на изменения цен друг друга.

Игры с одновременными ходами

Прежде чем предпринимать какие-то действия, в играх с одновременными ходами, игроки должны составить таблицу выплат. В ней количественно определяются последствия различных ходов, которые могут быть сделаны игроками-участниками.

Простейший пример: ситуация между двумя игроками, которые делают один ход, имея только два варианта этого хода и четыре возможных итога:

1. Оба игрока делают ход А.
2. Игрок 1 делает ход А, игрок 2 делает ход Б.
3. Игрок 1 делает ход Б, игрок 2 делает ход A.
4. Оба игрока делают ход Б.

• Например, это подходит для двух производителей виджетов, которые являются единственными конкурентами в нише. Каждый из них в настоящее время имеет 50% рынка и продажи в размере 2 млн долларов в год.
• С развитием в области компонентных технологий теперь у каждого из них появилась возможность разрабатывать виджеты следующего поколения, но вывод такого продукта на рынок, будет стоить 500 тысяч долларов.
• Если оба разработают новые виджеты, общий рынок вырастет на 10%, так как существующие клиенты захотят обновиться.
• Если только один разработает новый виджет, то компания увеличит свою долю рынка до 75%. Но общий рынок вырастет только на 5%, так как некоторые существующие клиенты останутся лояльными к поставщику, который не предлагает новый продукт.
• Если ни одна из компаний не разработает новый виджет, продажи останутся прежними.

Таблица выплат для этой ситуации показывает доход от продаж, который каждый игрок ожидал бы в первый год за каждый из четырех возможных итогов. (Результаты для Компании №1 показаны первыми, результаты для Компании №2 — вторыми ).

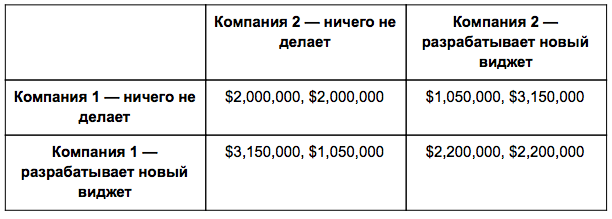
Однако необходимо учитывать и стоимость разработки нового виджета, поэтому в приведенной ниже таблице данная стоимость исключена из данных о продажах:

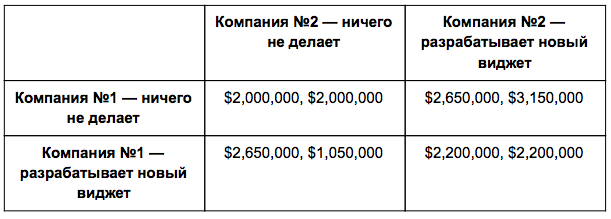
План действий для двух компаний

Понятно, что лучшим результатом для любой компании было бы разработать новый виджет, тогда как ее конкурент будет бездействовать. Но ни одна из них не может знать, что сделает другой.

Если одна из компаний ничего не предпримет, то её доходы могут упасть почти на 50%, при условии, что другая компания разработает новый продукт. С другой стороны, если она продолжить действовать, то бездействие другой компании, поставит её в выигрышную ситуацию; или она испытает относительно меньшее падение дохода после вычета стоимости разработки, если другая компания также движется вперед.

Оптимальное решение в данной ситуации — двигаться вперед. Но менеджерам следует быть осторожными, чтобы подготовиться к возможным негативным последствиям, которые могут произойти, если их конкуренты также будут разрабатывать новые продукты. По факту, если оба конкурента будут рационально анализировать ситуацию, есть вероятность, что оба разработают новый виджет и увидят падение прибыли в этом году.

Подсказка

Думая о том, что будет делать ваш конкурент, предположите, что она или он сделает для себя наилучший возможный выбор. Не думайте, что их решение будет случайным.

Дилемма заключенного

Игра «Дилемма заключенного» — классический пример теории игр. Двое заключенных содержатся в качестве подозреваемых в краже со взломом, и каждому из них предлагается следующая сделка:

1. Если ни один из заключенных не сознается в краже со взломом, каждый из них отправится в тюрьму на один год.
2. Если один заключенный признается и соглашается дать показания против другого, но другой не признается, то признавшийся заключенный выйдет на свободу, а молчаливый отправится в тюрьму на пять лет.
3. Если оба заключённых дадут признательные показания, то будут отбывать наказание в виде лишения свободы сроком на три года.

Для игр с одновременным ходом можно создать «таблицу выплат», которая показывает различные комбинации выбора. Записи в таблице показывают, сколько каждый игрок (заключенный) выигрывает или проигрывает в каждом случае.

Наша таблица выплат приведена ниже («-1» — означает один год тюремного заключения и т.д.):

Дилемма

Теоретически, наилучший вариант для каждого заключенного — ничего не говорить и получить по одному году тюрьмы. Проблема в том, что ни один из них не уверен, сознается ли другой, чтобы полностью избежать наказания. Поэтому оба заключенных, в конечном итоге, сознаются в преступлении и получат три года, а не один.

Игры с последовательными ходами и Дерево игр

Для игры с последовательными ходами, в которой игроки ходят по очереди, один за другим, вместо матрицы выплат создается «Дерево игры» (похожее на «Дерево принятия решений»). «Дерево игры» начинается с одной точки, а затем разветвляется на различные, возможные для первого игрока, ходы. Каждый из этих возможных ходов снова разветвляется, чтобы покрыть все возможные реакции на ход второго игрока, и так далее.

Большинство переговоров считаются Играми с последовательным ходом, и вы можете представить их с помощью «Дерева игры». Например, некая пекарня хочет приобрести новый фургон для доставки продуктов. Они обращаются к продавцу, который предлагает фургон, удовлетворяющий их потребностям, по цене 18 тысяч долларов.

Пекарня принимает первое решение. Есть три варианта:

• принять предложение;
• отклонить предложение;
• попросить лучшую цену.

В ответ на отказ продавец может уйти или сделать более выгодное предложение. В ответ на просьбу о лучшей цене, продавец может снизить цену или уйти, и так далее.

Обратная аргументация

«Деревья игр», описывающие Игры с последовательными ходами, также позволяют «смотреть вперед и рассуждать назад». Это позволяет увидеть, какой должна быть ваша стратегия сейчас, чтобы иметь наибольшие шансы на успех в будущем. Это также известно как обратная индукция.

Чтобы определить, как будет разворачиваться игра, начните с нижней части вашего дерева и двигайтесь по направлению вверх, предполагая, что что ваш оппонент каждый раз будет делать наилучший ход. В процессе «подрезайте» ветви дерева, которые отражают — проигрышный выбор. То, что у вас осталось, —  вероятный исход игры, если предположить, что ни один из игроков не совершит ошибку.

Возвращаясь к нашему простому примеру с пекарней: пекарня должна попросить лучшую цену, продавец должен согласиться на неё, а пекарня должна принять. Иначе, продавец потеряет продажу, а пекарня не сможет доставить свой хлеб. Конечно, такой вариант приемлем при условии, что продавцу нужна эта продажа, а у пекарни нет лучшего варианта.

Когда игры приходят в равновесие

Во многих ситуациях (но не всегда) игры оказываются в стабильной ситуации, известной в теории игр как «Равновесие Нэша» (названо в честь Джона Нэша, еще одного игрока в этой области). В данной ситуации игроки знают стратегии друг друга и делают наилучшие, для этих условий, ходы. После того, как они сделали эти ходы, ни один игрок не заинтересован в изменении своей стратегии.

Бизнес-пример

Компании, работающие на одном и том же рынке, стремятся максимизировать свою прибыль, выбирая для себя определенный уровень производства. Наилучший результат (и прибыль) для одной компании зависит от результата работы другой компании, поэтому ситуация стабилизируется в «Равновесии Нэша».

Имея дело с реальной жизнью

Теория игр адаптируется к дополнительным факторам в реальных жизненных ситуациях. Даже если она использует математические формулы для прогнозирования результатов, она также руководствуется здравым смыслом для оценки реального мира. Например, в «Дилемме заключенного», заключенные могут снова оказаться в той же ситуации, что и подозреваемые по второму делу о краже со взломом. Однако, в зависимости от того, как они действовали в первый раз, их действия в этот раз могут измениться — особенно если они пытаются избежать ошибок, которые совершили в прошлом.

Точно так же, размышляя о бизнесе, например, авиационной промышленности, мы можем выйти за рамки моделей, ограниченных изменением цен и конкуренцией между существующими авиакомпаниями. Мы можем использовать дополнительные возможности: выход на другой рынок конкурентов (например, лоукостеров) или клиентов, переходящих к другим решениям (ездить на поезде, телеконференции и т.д.). И определенный выбор, который делают авиакомпании, может привести к обвинениям в фиксации цен и антиконкурентной практике, которая также может быть смоделирована при помощи теории игр.

Больше ценных советов для перехода с позиции технического эксперта на менеджерскую позицию, вы можете найти в книге Маршалла Голдсмита «То, что привело вас сюда, не приведет вас туда».

Ключевые моменты

Теория игр помогает нам понять, как люди поступают и взаимодействуют: в бизнесе или социальной среде. Часть теории игр посвящена основным идеям, которые можно сразу же применить в реальной жизни. К ним относятся простые таблицы, показывающие результаты (выплаты) за различные варианты выбора, или древовидные диаграммы, которые следуют за несколькими этапами взаимодействия.

Рассматривая возможные результаты и работая в обратном направлении, вы можете выбрать стратегию, которая с наибольшей вероятностью даст вам наилучшие результаты.